Étude des systèmes du 2° ordre
La transmittance des systèmes du 2° ordre s'écrit sous la forme canonique suivante :
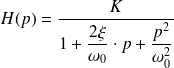
Avec
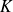 le gain statique,
le gain statique,
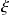 l'amortissement et
l'amortissement et
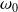 la pulsation propre non amortie.
la pulsation propre non amortie.
Étude informatique sous Scilab
Dans un premier temps, nous allons réaliser un programme Scilab permettant de tracer les réponses temporelles d'un système du second ordre à partir d'un programme sous Scilab.
Question
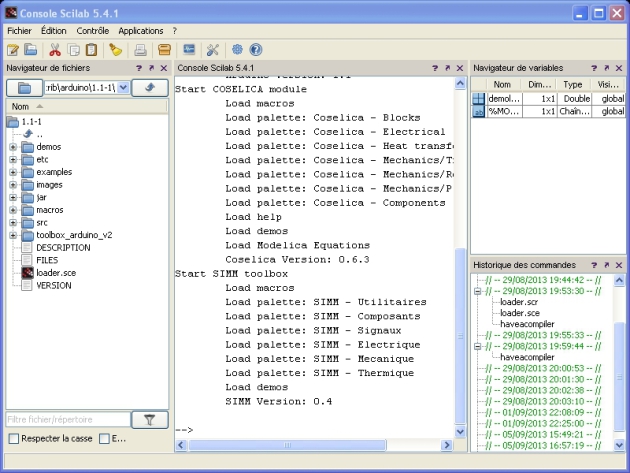
Lancez Scilab à partir de l’icône  , la fenêtre ci-dessous s'ouvre.
, la fenêtre ci-dessous s'ouvre.
La fenêtre Scilab est décomposée en 4 parties :
le navigateur de fichier à gauche,
la console au centre, zone dans laquelle vous pouvez entrer des lignes de code,
le navigateur de variable en haut à droite (liste des variables créée et utilisée),
l'historique des commandes en bas à droite.
Cliquez alors sur le bouton ![]() en haut à gauche de la fenêtre Scilab permettant d'ouvrir l'éditeur de programme Scilab nommé Scinotes ci dessous.
en haut à gauche de la fenêtre Scilab permettant d'ouvrir l'éditeur de programme Scilab nommé Scinotes ci dessous.
C'est dans cette fenêtre que vous allez éditer le programme permettant de tracer les réponses temporelles des systèmes du second ordre.
Réponse indicielle des systèmes du second ordre
Vous avez vu en 1° année PTSI que les systèmes du second ordre admettent 2 types de réponses indicielles (apériodique ou pseudo-périodique amortie) en fonction de la valeur de
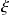 . Nous allons utiliser les fonctions de base de Scilab pour tracer ces réponses indicielles et vérifier le cours.
. Nous allons utiliser les fonctions de base de Scilab pour tracer ces réponses indicielles et vérifier le cours.
Afin de définir une fonction de transfert sous Scilab, il faut d'abord définir les polynômes en s (variable de Laplace pour les anglo-saxons), puis rentrer la fonction de transfert et spécifier au logiciel que c'est une fonction de transfert .
Un exemple est plus parlant qu'une explication, donc pour créer la fonction de transfert
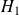 , on tape sur la fenêtre Scinotes :
, on tape sur la fenêtre Scinotes :
//définition du polynôme en s
s = poly(0,'s')
//définition de la fonction de transfert
H1 = syslin('c',[5],[2*s^2+0.2*s+1])
Le double // correspond à un commentaire...
Si vous lancez la simulation à partir du bouton ![]() , Scilab créé la variable H1 visible dans le navigateur de variable, vous pouvez visualiser cette variable en tapant H1 dans la console Scilab et en validant par Entrée :
, Scilab créé la variable H1 visible dans le navigateur de variable, vous pouvez visualiser cette variable en tapant H1 dans la console Scilab et en validant par Entrée :
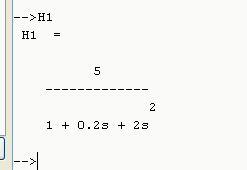
Il est possible aussi de réaliser des boucles en utilisant la syntaxe for end, là aussi, un exemple est plus parlant :
for i=1:0.5:10
disp(i)
end
Afin de tracer une courbe, il faut utiliser la fonction plot ou plot2d, essayons sur un exemple :
//création d'une fenêtre de courbe
f1=scf(1)
//création d'un vecteur temps
t=0:0.1 :10
//tracé de la courbe
plot2d(t,csim('step',t,H1),3)
Vous pouvez taper help plot2d pour avoir une aide et des exemples sur la fonction plot2d, vous pouvez d'ailleurs faire cela pour toutes les fonctions Scilab. La fonction csim permet de simuler la réponse temporelle d'un système linéaire à partir de la connaissance de sa fonction de transfert, si l'on désire tracer une courbe à partir de son équation temporelle, il suffit de taper par exemple pour la fonction sinus :
plot2d(t,sin(t),5)
Question
A partir des exemples de programme précédents, réalisez un programme permettant d'afficher sur une première fenêtre la réponse à un échelon pour un système du second ordre pour
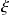 variant de 1 à 10 avec un pas de 1.
variant de 1 à 10 avec un pas de 1.
Afin de simplifier le tracé, vous pourrez définir une variable temps réduit, notée
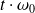 variant de 0 à 20 avec un pas de 0.01 s.
variant de 0 à 20 avec un pas de 0.01 s.
//Définition de la variable de Laplace s et polynome en s
s = poly(0,'s')
// Cas du régime apériodique
f1=scf(1)
two=0:0.01:20
for z=1:10
// Définition du système linéaire défini par la fonction de transfert H2
H2 = syslin('c',[2],[s^2+2*z*s+1])
plot2d(two,csim('step',two,H2),z)
end
xgrid(14)
xtitle("Régime apériodique")
legend(["1","2","3","4","5","6","7","8","9","10"],1)
Question
A partir des exemples de programme précédents, réalisez un programme permettant d'afficher sur une deuxième fenêtre la réponse à un échelon pour un système du second ordre pour
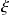 variant de 0.1 à 1 avec un pas de 0.1.
variant de 0.1 à 1 avec un pas de 0.1.
Afin de simplifier le tracé, vous pourrez définir une variable temps réduit, notée
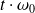 variant de 0 à 10 avec un pas de 0.01 s.
variant de 0 à 10 avec un pas de 0.01 s.
//Cas du régime pseudopériodique
f2=scf(2)
two=0:0.01:10
for z=0.1:0.1:1
H2 = syslin('c',[2],[s^2+2*z*s+1])
plot2d(two,csim('step',two,H2),10*z)
end
xgrid(14)
xtitle("Régime pseudopériodique")
legend(["0.1","0.2","0.3","0.4","0.5","0.6","0.7","0.8","0.9","1"],1)
Il est possible de créer des fonctions afin de les appeler ensuite dans un programme, vous pourrez avoir des informations concernant cette fonction en tapant help function dans la console de commande de Scilab.
Question
Question
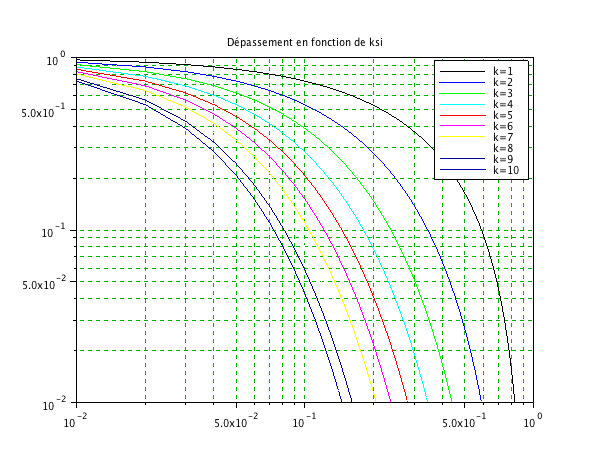
A partir de la fonction précédente, réalisez un programme permettant d'afficher sur une troisième fenêtre le tracé des dépassement en fonction de l'amortissement
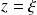 . Vous ferez varier
. Vous ferez varier
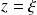 entre les valeurs 0.01 et 0.99 avec un pas de 0.01, vous afficherez les courbes pour les 10 premiers dépassements.
entre les valeurs 0.01 et 0.99 avec un pas de 0.01, vous afficherez les courbes pour les 10 premiers dépassements.
La courbe doit être affichée en échelle Log-Log, vous pouvez obtenir des informations sur les graphes en tapant dans la console help plot2d.
//Tracé du dépassement en fonction de ksi
f3=scf(3)
z=0.01:0.01:0.99
for k=1:10
f=[]
for x=0.01:0.01:0.99
f=[f,D(k,x)]
end
plot2d("ll",z,f,style=k,strf="011",rect=[0.01,0.01,1,1])
end
xgrid(14)
xtitle("Dépassement en fonction de ksi")
legend(["k=1","k=2","k=3","k=4","k=5","k=6","k=7","k=8","k=9","k=10"],1)
Question
Copiez le listing ci-dessous dans Scinotes et exécutez le programme.
clear
// Question 1
function r=s(two,z)
b=z**2-1
if z>1 then
a=sqrt(b) ;
r=1+exp(-two*(z+a))*(1/2/(z*a+b))-exp(-two*(z-a))*(1/2/(z*a-b))
else if z<1 then
a=sqrt(-b) ;
r=1-exp(-two*z)/a*sin(two*a+asin(a))
else if z==1 then
r=1-(1+two)*exp(-two)
end
end
end
endfunction
// Question 2
f1=scf(1)
two=0:0.01:10
for z=1:10
f=[]
for x=0:0.01:10
f=[f,s(x,z)]
end
plot2d(two,f,style=z)
end
xgrid(14)
xtitle("Régime apériodique")
legend(["1","2","3","4","5","6","7","8","9","10"],1)
// Question 3
f2=scf(2)
two=0:0.01:10
for z=0.1:0.1:1
f=[]
for x=0:0.01:10
f=[f,s(x,z)]
end
plot2d(two,f,style=z*10)
end
xgrid(14)
xtitle("Régime apériodique")
legend(["1","2","3","4","5","6","7","8","9","10"],1)
// Question 4
function r=dans_bande(v)
if v>=0.95 & v<=1.05 then
r=1
else
r=0
end
endfunction
// Question 5
liste_z=[]
liste_trwo=[]
pas_z=0.01
pas_two=0.05
//z<0.6
//On teste la sortie de bande en partant d'une valeur de two suffisamment grande.
//Le temps de réponse réduit étant décroissant, on peut à chaque itération de z,
//repartir avec la dernière valeur de trwo déterminée.
two=400
z=0.01
while z<0.6
while dans_bande(s(two,z))
two=two-pas_two
end
two=two+pas_two ;
liste_z=[liste_z,z] ;
liste_trwo=[liste_trwo,two] ;
z=z+pas_z
end
//z>0.6 et z<=1
//On teste la sortie de bande en partant d'une valeur de two suffisamment grande.
//A chaque itération de z, on prend two=7 comme valeur de départ.
z=0.6
while z<=1
two=7 ;
while dans_bande(s(two,z))
two=two-pas_two
end
two=two+pas_two
liste_z=[liste_z,z] ;
liste_trwo=[liste_trwo,two] ;
z=z+pas_z
end
// z>=1
//On teste l'entrée de bande en partant d'une valeur de two suffisamment petite.
//Le temps de réponse réduit étant croissant, on peut à chaque itération de z,
//repartir avec la dernière valeur de trwo déterminée.
z=1
two=0
while z<50
while ~(dans_bande(s(two,z)))
two=two+pas_two
end
two=two-pas_two
liste_z=[liste_z,z] ;
liste_trwo=[liste_trwo,two] ;
z=z+pas_z
end
f3=scf(3)
plot2d(liste_z,liste_trwo,logflag="ll")
xgrid(14)
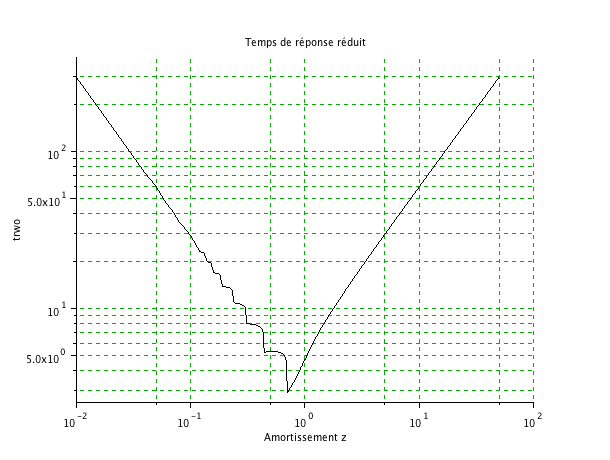
xtitle("Temps de réponse réduit","Amortissement z","trwo")
Vous obtenez alors un tracé de l'abaque de temps de réponse réduit. Expliquez la forme de la courbe.
Étude des fonctions du 2° ordre à partir de Xcos
Le module Xcos est accessible à partir du bouton ![]() , après appui sur ce bouton, une fenêtre vierge de travail s'ouvre et le navigateur de palette apparaît.
, après appui sur ce bouton, une fenêtre vierge de travail s'ouvre et le navigateur de palette apparaît.
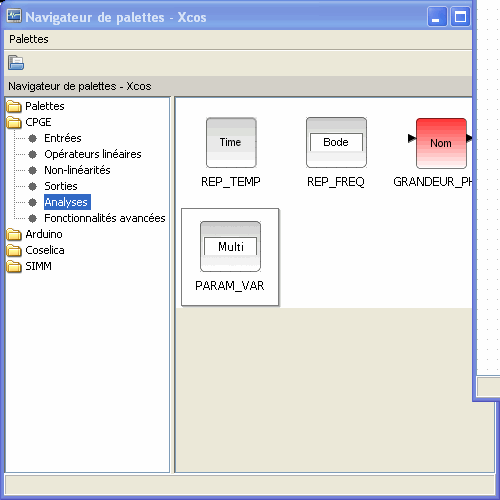
Nous utiliserons plus particulièrement les modèles du module CPGE mais il est tout à fait possible d'utiliser les modèles des autres module si besoin est. Afin de réaliser un modèle, il faut d"finir la durée de simulation, pour cela, il faut insérer le modèle REP_TEMP sur le modèle créé.
Question
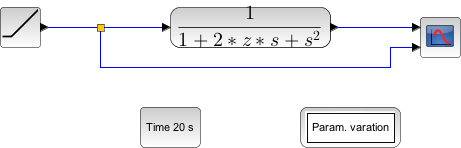
En important sur votre feuille vierge Xcos les éléments Step_function, CLR, Scope, Rep_temp, créez un schéma bloc correspondant à la fonction de transfert définie ci-dessous.
Dans un premier temps, nous allons vérifier les caractéristiques générales de la réponse à un échelon
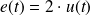 pour le système du 2° ordre ci-dessus.
pour le système du 2° ordre ci-dessus.
Tracez la réponse temporelle de cette fonction et retrouvez les caractéristiques
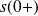 ,
,
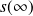 et la tangente à l'origine.
et la tangente à l'origine.

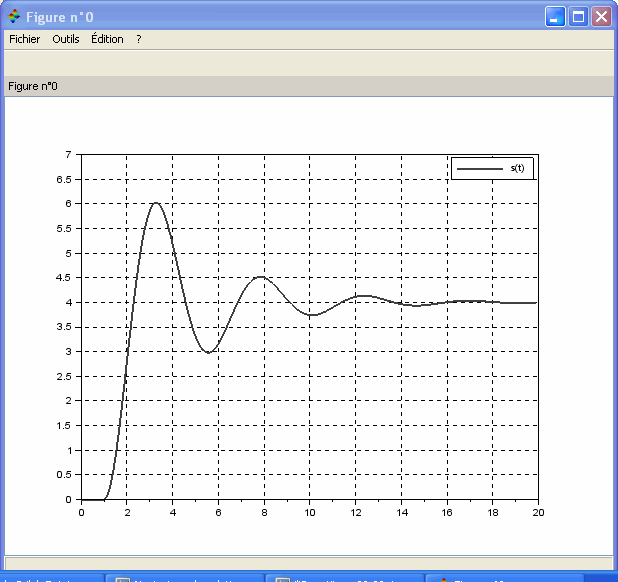
On désire à présent étudier l'effet d'une variation de
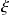 et de
et de
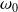 sur la réponse du système du second ordre. Pour cela, nous allons utiliser le modèle PARAM_VAR disponible dans le module CPGE, section Analyse. Afin d'utiliser ce bloc, il faut au préalable définir les paramètres variables. Pour cela, il faut aller dans le menu Simulation et sélectionner Modifier le contexte, vous pouvez alors définir les paramètres symboliques que vous voulez intégrer dans votre modèle.
sur la réponse du système du second ordre. Pour cela, nous allons utiliser le modèle PARAM_VAR disponible dans le module CPGE, section Analyse. Afin d'utiliser ce bloc, il faut au préalable définir les paramètres variables. Pour cela, il faut aller dans le menu Simulation et sélectionner Modifier le contexte, vous pouvez alors définir les paramètres symboliques que vous voulez intégrer dans votre modèle.
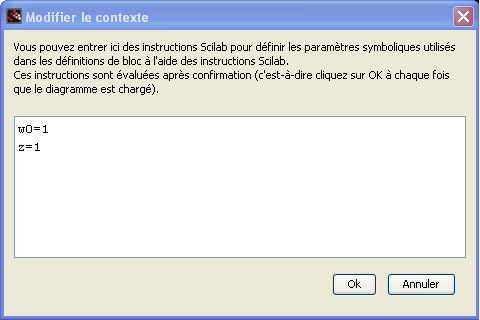
Modifiez votre schéma bloc à partir de Xcos afin d'introduire
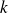 ,
,
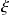 et
et
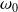 variables.
variables.

Question
Nous désirons étudier l'effet de l'amortissement
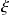 . Afin de faciliter l'introduction des valeurs dans Xcos, nous allons choisir une pulsation propre non amortie de
. Afin de faciliter l'introduction des valeurs dans Xcos, nous allons choisir une pulsation propre non amortie de
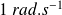 . On prendra
. On prendra
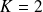 et
et
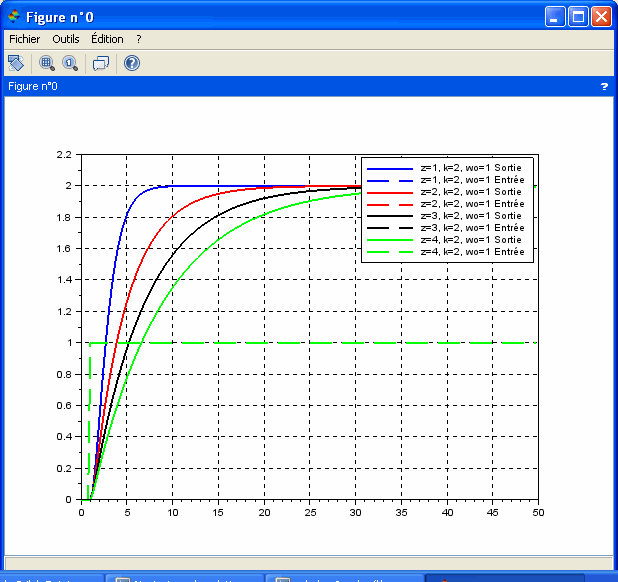
 variable. Conclure quant à l'effet de l'amortissement sur la forme de la réponse. Effectuez un zoom sur l'origine et conclure quant à la tangente à l'origine dans le cas d'un système du second ordre.
variable. Conclure quant à l'effet de l'amortissement sur la forme de la réponse. Effectuez un zoom sur l'origine et conclure quant à la tangente à l'origine dans le cas d'un système du second ordre.
Question
Dans le cas de
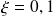 , mesurez la pseudo-période et comparez cette pseudo-période avec celle que vous avez calculé à partir de la relation du cours. Conclure. Donnez la valeur de l'instant du premier dépassement en fonction de la pseudo-période du système.
, mesurez la pseudo-période et comparez cette pseudo-période avec celle que vous avez calculé à partir de la relation du cours. Conclure. Donnez la valeur de l'instant du premier dépassement en fonction de la pseudo-période du système.
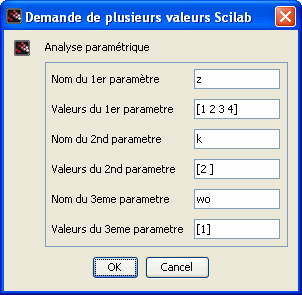
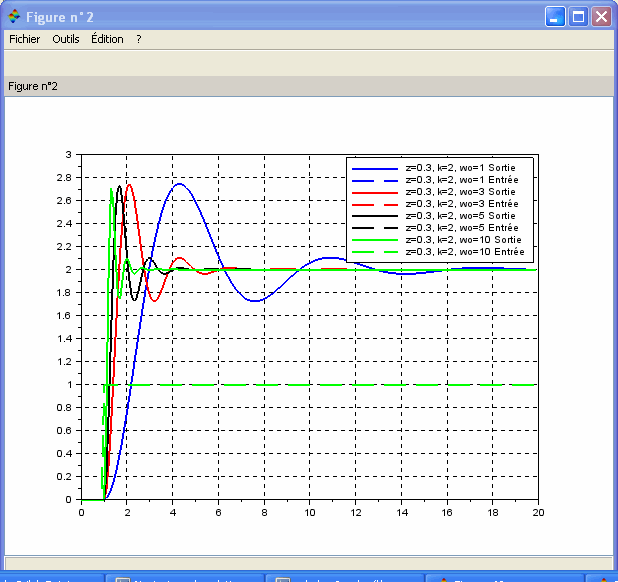
On s'intéresse à présent à l'influence de la pulsation propre non amortie sur la forme de la réponse à un échelon.
Pour
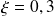 , tracez les réponses à un échelon pour différentes valeurs de la pulsation propre non amortie
, tracez les réponses à un échelon pour différentes valeurs de la pulsation propre non amortie
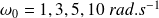 . Conclure quant à l'effet de la pulsation propre amortie sur la forme de la réponse à un échelon pour un système du 2° ordre (temps de réponse, dépassement).
. Conclure quant à l'effet de la pulsation propre amortie sur la forme de la réponse à un échelon pour un système du 2° ordre (temps de réponse, dépassement).
Question
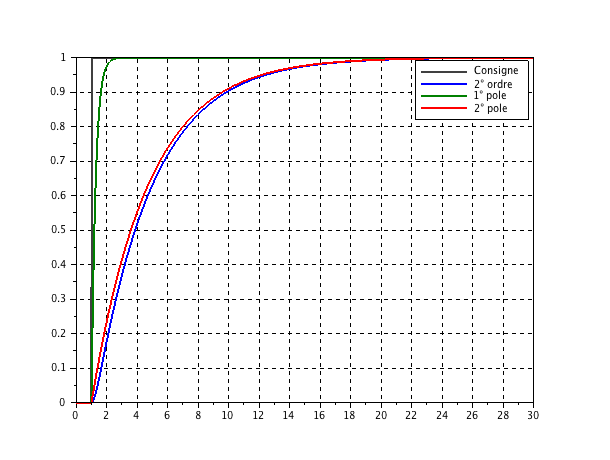
Dans le cas où
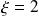 ,
,
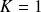 et
et
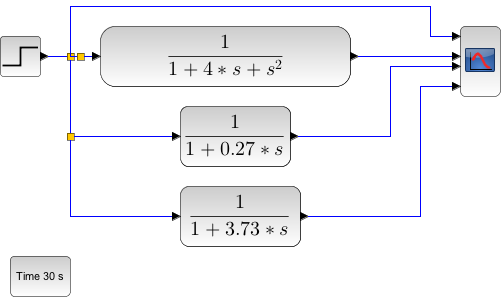
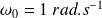 , déterminez les pôles de la fonction de transfert et tracez la réponse à cette fonction de transfert sous la forme d'un produit de deux 1° ordre et sous la forme d'un second ordre. Conclure.
, déterminez les pôles de la fonction de transfert et tracez la réponse à cette fonction de transfert sous la forme d'un produit de deux 1° ordre et sous la forme d'un second ordre. Conclure.
Déterminez les deux fonctions du premier ordre définies à partir des deux pôles précédents (veillez à garder un gain unitaire pour toutes ces fonctions de transfert). Tracez ensuite la réponse temporelle à un échelon pour les deux fonctions de premier ordre séparément (attention au gain), comparez les réponses temporelles avec celle de la fonction du second ordre produit des deux premières. Conclure.
Vous pouvez repartir du schéma bloc précédent, il suffit alors de rajouter des entrées sur le Scope (double clic) et de réaliser 3 branches en parallèles avec d'une part le système du second ordre et d'autre part, les deux systèmes du 1° ordre.
Question
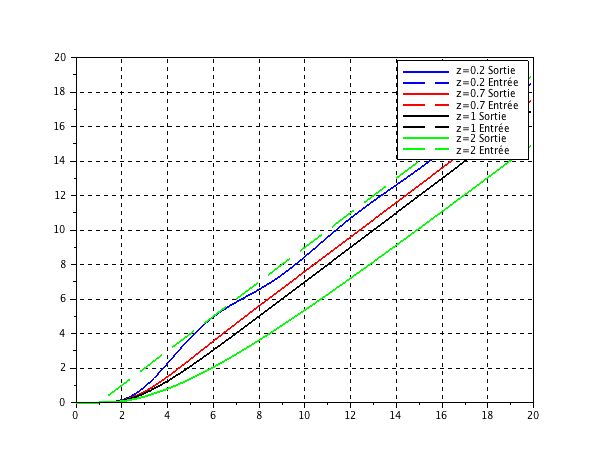
On s'intéresse à présent à la réponse à une rampe pour un système du 2° ordre. Choisissez une rampe unitaire et un gain statique de 1 pour votre fonction de transfert. Tracez les réponses à une rampe pour des fonctions du second ordre avec
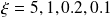 . Quelles conclusions pouvez vous déduire de ces courbes ? Est-il facile d'identifier un système du second ordre grâce à sa réponse à une rampe ?
. Quelles conclusions pouvez vous déduire de ces courbes ? Est-il facile d'identifier un système du second ordre grâce à sa réponse à une rampe ?
Vous pouvez partir du tracé pour un échelon et il suffit de remplacer l'échelon par une rampe.
 Exercice : Étude des systèmes du 1° ordre
Exercice : Étude des systèmes du 1° ordre